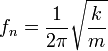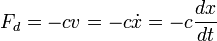Setiap gerak yang terjadi secara berulang dalam selang waktu yang sama disebut gerak periodik. Karena gerak ini terjadi secara teratur maka disebut juga sebagai gerak harmonik/harmonis. Apabila suatu partikel melakukan gerak periodik pada lintasan yang sama maka geraknya disebut gerak osilasi/getaran. Bentuk yang sederhana dari gerak periodik adalah benda yang berosilasi pada ujung pegas. Karenanya kita menyebutnya gerak harmonis sederhana. Banyak jenis gerak lain (osilasi dawai, roda keseimbangan arloji, atom dalam molekul, dan sebagainya) yang mirip dengan jenis gerakan ini, sehingga pada kesempatan ini kita akan membahasnya secara mendetail.
Dalam kehidupan sehari-hari, gerak bolak balik benda yang bergetar terjadi tidak tepat sama karena pengaruh gaya gesekan. Ketika kita memainkan gitar, senar gitar tersebut akan berhenti bergetar apabila kita menghentikan petikan. Demikian juga bandul yang berhenti berayun jika tidak digerakan secara berulang. Hal ini disebabkan karena adanya gaya gesekan. Gaya gesekan menyebabkan benda-benda tersebut berhenti berosilasi. Jenis getaran seperti ini disebut getaran harmonik teredam. Walaupun kita tidak dapat menghindari gesekan, kita dapat meniadakan efek redaman dengan menambahkan energi ke dalam sistem yang berosilasi untuk mengisi kembali energi yang hilang akibat gesekan, salah satu contohnya adalah pegas dalam arloji yang sering kita pakai. Pada kesempatan ini kita hanya membahas gerak harmonik sederhana secara mendetail, karena dalam kehidupan sehari-hari terdapat banyak jenis gerak yang menyerupai sistem ini.
GERAK HARMONIS SEDERHANA
Gerak harmonis sederhana yang dapat dijumpai dalam kehidupan sehari-hari adalah getaran benda pada pegas dan getaran benda pada ayunan sederhana. Kita akan mempelajarinya satu persatu.
Gerak Harmonis Sederhana pada Ayunan

Ketika beban digantungkan pada ayunan dan tidak diberikan gaya maka benda akan diam di titik kesetimbangan B. Jika beban ditarik ke titik A dan dilepaskan, maka beban akan bergerak ke B, C, lalu kembali lagi ke A. Gerakan beban akan terjadi berulang secara periodik, dengan kata lain beban pada ayunan di atas melakukan gerak harmonik sederhana.
Besaran fisika pada Gerak Harmonik Sederhana pada ayunan sederhana
Periode (T)
Benda yang bergerak harmonis sederhana pada ayunan sederhana memiliki periode alias waktu yang dibutuhkan benda untuk melakukan satu getaran secara lengkap. Benda melakukan getaran secara lengkap apabila benda mulai bergerak dari titik di mana benda tersebut dilepaskan dan kembali lagi ke titik tersebut.
Pada contoh di atas, benda mulai bergerak dari titik A lalu ke titik B, titik C dan kembali lagi ke B dan A. Urutannya adalah A-B-C-B-A. Seandainya benda dilepaskan dari titik C maka urutan gerakannya adalah C-B-A-B-C.
Jadi periode ayunan (T) adalah waktu yang diperlukan benda untuk melakukan satu getaran (disebut satu getaran jika benda bergerak dari titik di mana benda tersebut mulai bergerak dan kembali lagi ke titik tersebut ). Satuan periode adalah sekon atau detik.
Frekuensi (f)
Selain periode, terdapat juga frekuensi alias banyaknya getaran yang dilakukan oleh benda selama satu detik. Yang dimaksudkan dengan getaran di sini adalah getaran lengkap. Satuan frekuensi adalah 1/sekon atau s-1. 1/sekon atau s-1 disebut juga hertz, menghargai seorang fisikawan. Hertz adalah nama seorang fisikawan tempo doeloe. Silahkan baca biografinya untuk mengenal almahrum eyang Hertz lebih dekat.
Hubungan antara Periode dan Frekuensi
Frekuensi adalah banyaknya getaran yang terjadi selama satu detik/sekon. Dengan demikian selang waktu yang dibutuhkan untuk melakukan satu getaran adalah :

Selang waktu yang dibutuhkan untuk melakukan satu getaran adalah periode. Dengan demikian, secara matematis hubungan antara periode dan frekuensi adalah sebagai berikut :

Amplitudo (f)
Pada ayunan sederhana, selain periode dan frekuensi, terdapat juga amplitudo. Amplitudo adalah perpindahan maksimum dari titik kesetimbangan. Pada contoh ayunan sederhana sesuai dengan gambar di atas, amplitudo getaran adalah jarak AB atau BC.
 Pernahkah anda menonton permainan biliard ? lebih baik lagi jika dirimu adalah pemain biliard
Pernahkah anda menonton permainan biliard ? lebih baik lagi jika dirimu adalah pemain biliard